شرح جمع وطرح الكسور مع شيتات مصورة
هنقدم شرح جمع وطرح الكسور مع شيتات مصورة بيصعب على اولياء الامور شرحها لاولادهم فى هذا المقال شرح وافى وشيتات بامثلة تجعلكم باذن الله تتمكنوا من هذا الدرس
في عملية جمع وطرح الكسور العادية يمكن ان نميز بين ثلاثة حالات قد تظهر فيها الكسور:
شرح جمع وطرح الكسور مع شيتات مصورة
الحالة الاولى
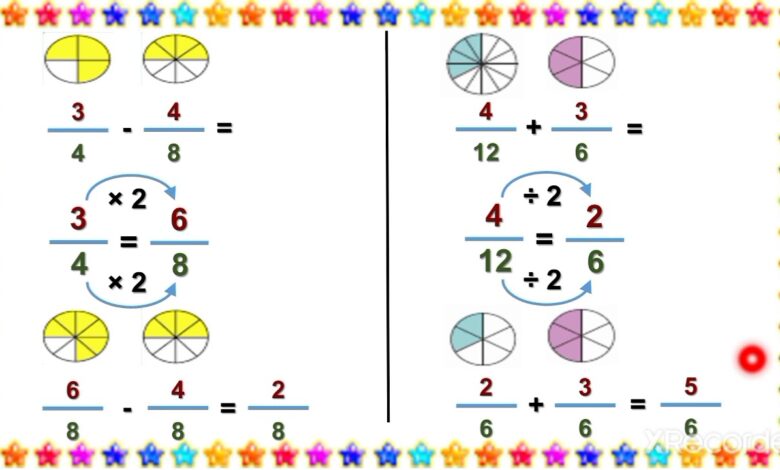
كسور ذات مقامات متشابهة مثل 5/1 5/3 وعندها طرح او جمع هذه الكسور يتم عن طريق جمع او طرح
البسط
والمقام يبقى ثابتًا. فبجمع الكسرين المعطيين نحصل على 5/4، وبطرحهن نحصل على 5/2.


جمع وطرح الكسور ذات المقامات المختلفة
الحالة الثانية:
كسور ذات مقامات محوية: اي ان احد المقامات تقبل القسمة على الاخر بدون باقي مثل 5/4 3/10 فالـ 10 تقسم على 5، (كما تعلمنا في توسيع واختزال الكسور)
يمكننا انو نوسع الكسر 5/4 ونضربه بـ2 ليصبح 10/8 وعندها يمكننا ان نحصل على النوع الاول (كسور ذات مقامات متساوية).


الحالة الثالثة:
كسور ذات مقامات مختلفة غريبة: بمعنى انها غير محوية، اي ان الاعداد في المقامات لا تقبل القسمة على بعضها
مثل : 3/1 و 5/3 فال 3 وال 5 عددان غريبان، فماذا نفعل في هذه الحالة؟


عند جمع و طرح كسور ذات مقامات لا تقبل القسمة على بعضها، نجد المضاعف المشترك البسيط ( الاصغر )
للاعداد التي تظهر في المقام. وهو اصغر عدد يقسم على المقامين بدون باقٍ.
فالمضاعف المشترك الاصغر للـ 5 والـ 3 هو 15، نوسع الكسر الاول بـ 3 لنحصل على مقام 15، والكسر الثاني بـ 5 لنحصل على 15:
3/5 * 3 = 9/15 ، 1/3 * 5 = 5/15 : وبهذه الطريقة نحصل على الحالة الاولى البسيطة.
في الأعلى نقوم بعملية توحيد لمقامين مختلفين بالقيمة حيث نضرب مقام العدد الأول بالعدد الثاني ومقام العدد الثاني بالعدد الأول.
في الرياضيات هو كتابة الكسور النسبية بشكل يكون فيه قيمة مقام الكسر موحدة.
بحيث تصبح عمليات الجمع والطرح بينهما صحيحة، إذ لا يجوز تطبيق عمليات الطرح البسيطة بين بسطي كسرين دون توحيد المقامات.
تعرف أيضا عملية توحيد المقامات بإيجاد قاسم مشترك بين أرقام كسرية، على سبيل المثال يسهل تمثيل كسور بأثمان تجمع وتطرح من أثمان على تمثيل كسور تمثل أنصاف تجمع إليها أثمان أو تطرح منها
و بالتالي، فإن تحويل النصف إلى ما يكافئه من الأثمان، وهم أربعة أثمان يسهل حساب مجموع النصف وثلاثة أثمان
حيث يكون الجواب بالأثمان، وهو حاصل جمع أربعة أثمان وثلاثة أثمان، أي سبعة أثمان.
يمكن توحيد المقامات بأكثر من طريقة، ويعتبر ضرب بسط ومقام الكسر الأول بمقام الكسر الثاني وضرب بسط
ومقام الكسر الثاني بمقام الأول أسهلها من حيث التطبيق، فبما أن الضرب عملية تبديلية، فإن المقام الأول مضروبا بالمقام الثاني سيساوي المقام الثاني مضروبا بالأول، وبالتالي يتحقق توحيد المقامين.
يمكن توحيد المقامات بأي عملية ضرب أو قسمة تطبّق على كل من بسط ومقام الكسر
فمثلا، مجموع الكسرين 2/6 و 4/3 يمكن تبسيط الأول إلى 1/3 بقسمة كل من البسط والمقام على 2
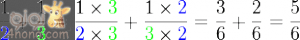
وبالتالي يتم توحيد المقامات بين الكسرين (وقيمة المقام في هذه الحالة 3) ويمكن جمع قيم البسطين 1 و 4 فيكون الكسر الناتج 5/3.




